Chameleon Mathematics

Chameleons, with their remarkable ability to adapt and blend into their surroundings, have found an intriguing presence in mathematical science through the concept of "chameleon fields." In theoretical physics and cosmology, chameleon fields are hypothetical scalar fields that exhibit variable properties, similar to how real chameleons change color. These fields play a significant role in theories related to dark energy, modified gravity, and the expansion of the universe. By borrowing from the chameleon's adaptive nature, mathematicians and physicists have created theoretical frameworks that dynamically evolve to match observations, mirroring the chameleon's ability to adjust seamlessly to diverse environments.

Mathematicians propose model for the dynamics of the chameleon tongue

Chameleons have captivated mathematicians with their extraordinary tongues. Scientists at Oxford University1 built a mathematical model to explain the secrets of the chameleon's powerful tongue. Here's what they discovered:

1. Speed and Extension: A chameleon's tongue unravels at a speed that would make a car go from 0 to 60 mph in just one hundredth of a second! It can extend up to 2.5 body lengths when catching insects.

2. Mathematical Insights: The researchers used differential equations to capture the mechanics of energy build-up and extreme acceleration in the reptile's tongue. At its core, this involves balancing forces with accelerations, based on Newton's Second Law.

3. Collagenous Tissue: Special collagenous tissue within the chameleon's tongue plays a crucial role. It surrounds a bone at the core of the tongue and is enveloped by muscle. The outermost muscle layer contracts to set the whole process in motion.

4. Biomimetics: These insights are valuable for biomimetics—copying nature's designs in engineering and design. Chameleons inspire us to create more efficient and powerful mechanisms based on their remarkable adaptations.

Chameleon: the most hidden chaotic flow

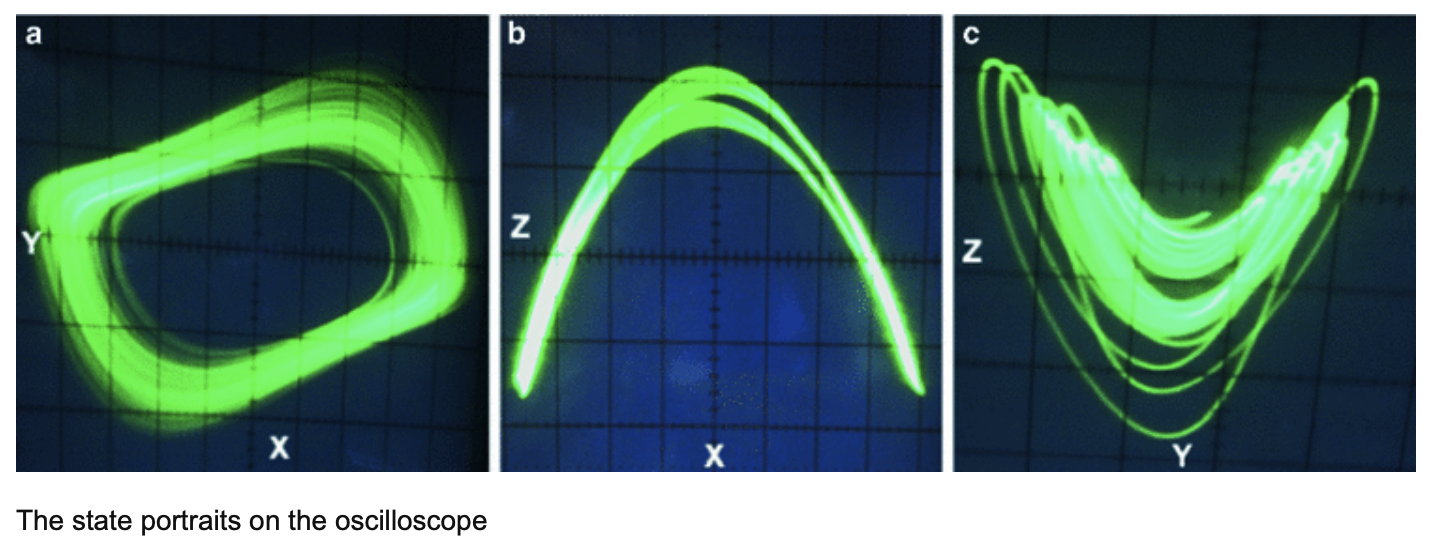
The image of a chameleon embodies the concept of hidden chaotic flow, where seemingly calm exteriors mask complex, unpredictable dynamics underneath. Much like how a chameleon's appearance can change rapidly to match its environment, hidden chaotic flows exhibit intricate patterns and behaviors that defy simple prediction or understanding. These flows, whether in nature, mathematics, or other systems, illustrate the intricate interplay between stability and turbulence, order and disorder, adding a layer of complexity that requires careful observation and analysis to unravel their true nature and implications.

Other Chameleon Mathematics Reading

Chameleon Riddles & Games

Chameleon mathematical riddles add an intriguing twist by combining the adaptive nature of chameleons with the precision and logic of mathematics. These riddles challenge the solver to think critically and apply mathematical concepts to uncover the answer. Here are three examples of chameleon mathematical riddles: